转转转

前置：BST

BST全称二叉搜索树，满足一个节点的左子树中的所有元素均比它自己小，右子树中元素都比它大。建树是要插入INF和-INF来确保查不到时返回的一定是不会取到的值，同时还有避免越界减少特判的作用。

但是，BST有一个缺点是当数据单调递增或递减时，树会退化成链导致不平衡，导致复杂度为O(n)。因此，需要一种操作来维持其平衡，于是就有了平衡树

第一种平衡树：SPlay

PlayU

SPlay有两种转法，这两种转法取决于三个因素

懒得打了，直接粘Wiki

• Whether x is the left or right child of its parent node, p,
• whether p is the root or not, and if not
• whether p is the left or right child of its parent, g (the grandparent of x).

注意事项

It is important to remember to set gg (the great-grandparent of x) to now point to x after any splay operation. If gg is null, then x obviously is now the root and must be updated as such.

基操：转

把父亲节点连带它的儿子一块怼成当前节点的左/右儿子（左旋就是左儿子），同时把原来的左/右儿子连到转成儿子的父亲节点上


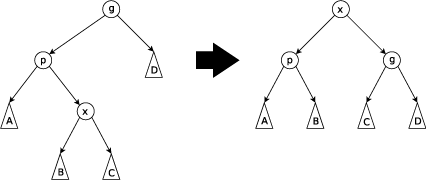
第一种转法：Zig-Zig 可以为全向右转，也可以为全向左转，适用于当前节点和父亲节点均为左右儿子的情况

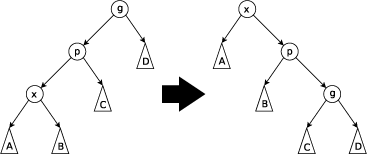
第二种转法：Zig-Zag 向左向右转（认真的）适用于当前节点和父亲节点左右儿子情况相反的情况

GUGUGUGUGU