1. 费马小定理

假如p是质数，且 $gcd(a,p)=1$，那么 $a^{(p-1)}≡1(mod p)$

证明：为欧拉定理的特殊情况。

用途：

降幂，比如说求 $ 2^{35} mod 7 $

由费马小定理可得 $ 2^{(7-1)} \equiv 1 mod p $

所以 $ 2^{6*k} \equiv 1 mod p $

原式为 $ 2^{65 + 2} mod 7 = 111112^2 mod 7 = 2^{0*5+2} mod 7 = 2^{35 mod (7-1) = 2} mod 7 $

所以 $ a^x mod p = a^{x mod (p-1)} mod p $ p为质数

2.欧拉定理

$ \varphi(p) = p-1 $

若a与m互质，则 $ a^{\varphi (m)} \equiv 1(mod m) $

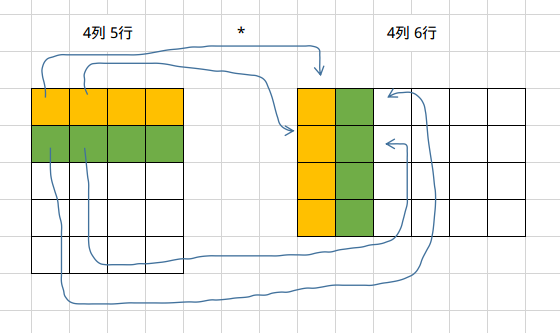
3. 矩阵乘法

相乘的第一个矩阵的列数必须等于被乘的矩阵的行数