noip模拟6

06-10-2021 约 1182 字预计阅读 3 分钟

~~挂分之神~~

T1

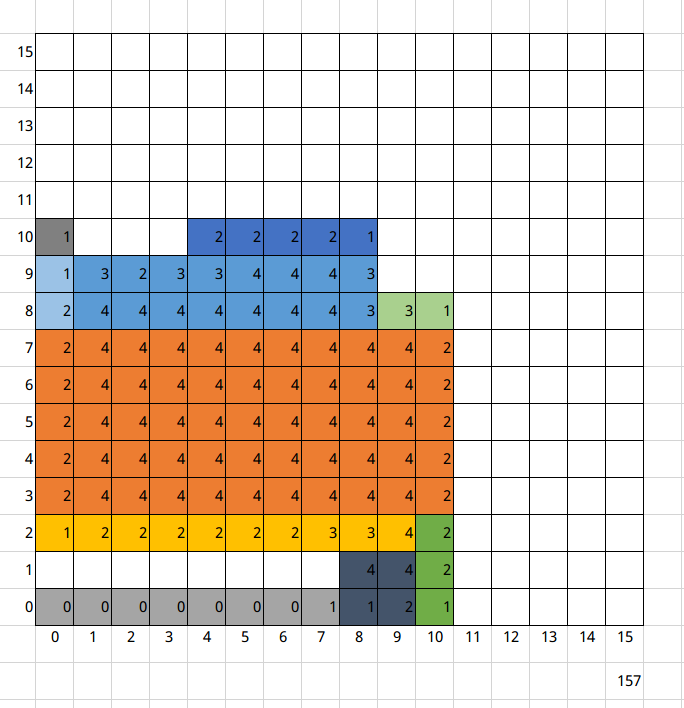
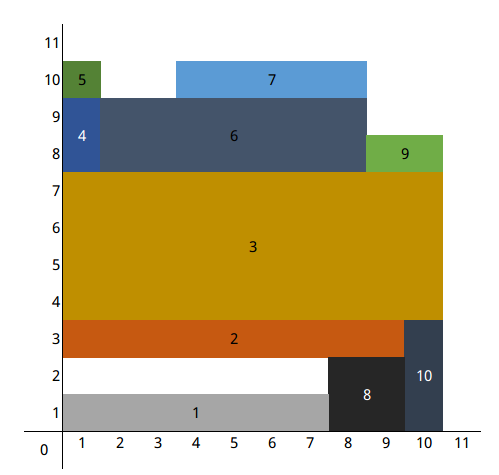
考场上是这么想的：先按x从小到大，再按y从小到大排序，然后从后往前枚举长方形看是否相邻，然后因为x和y越往前越小，所以可以剪枝。code

排完序的图片

然而，这种做法有一个大问题，就是随着i的增大，枚举的长方形数也会增大，而且我还是用枚举边框上的元素的方式来更新的结果，所以就出现了 $ {\color{Orange} \mathsf{TLE}} $ 然后在调代码时给我来了个这

emmm……既然从后往前不行那就从前往后，Nie！然后因为x随i（编号）增大而单调递增，所以对于水平方向来说只用看y，而竖直方向上只要x[j]=x[i]+1就可以转移，而且知道一个长方形内氢键的个数即为 $ (x_j - x_i)*(y_j - y_i) * 2 $ 那就好办了。

对于水平方向来说只用判断下一个长方形是否满足 $ y_j1 = y_x2+1 $ 或 $ y_j2 + 1 = y_x1 $ (分别对应上和下) 但还要注意若 $ x_i1=x_j1 $ (对x2同理)是要把ans-1（因为是斜线），竖直方向同理

code:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54


#include <bits/stdc++.h>
#define TO_BE_CONTINUED continue
using namespace std;
const int maxn(100010);

int n;
unsigned long long tot;
struct SQU {
  long long x1, y1, x2, y2;
} sq[maxn];
bool cmp(SQU a, SQU b) {
  if (a.x1 == b.x1) return a.y1 < b.y1;
  return a.x1 < b.x1;
}
int main() {
  // freopen("1.in", "r", stdin);
  scanf("%d", &n);
  for (int i = 1; i <= n; i++) {
    scanf("%lld%lld%lld%lld", &sq[i].x1, &sq[i].y1, &sq[i].x2, &sq[i].y2);
  }
  sort(sq + 1, sq + 1 + n, cmp);
  for (int i = 1; i <= n; i++) {
    tot += (sq[i].x2 - sq[i].x1) * (sq[i].y2 - sq[i].y1) * 4;
  }
  for (int i = 1; i <= n; i++) {
    if (n == 1) {
      cout << tot / 2 << endl;
      return 0;
    }
    for (int j = i + 1; j <= n; j++) {
      bool flagh = 0, flagv = 0;
      if (sq[j].x1 - sq[i].x2 > 1) break;
      if (sq[j].y1 - sq[i].y2 > 1) continue;
      if (sq[i].y1 - sq[j].y2 > 1) continue;
      if (sq[i].y2 + 1 == sq[j].y1 || sq[j].y2 + 1 == sq[i].y1) {  // horizontal
        if (sq[j].x1 == sq[i].x2 + 1) {
          tot += 2;
          TO_BE_CONTINUED;
        }
        tot += 4 * (min(sq[i].x2, sq[j].x2) - sq[j].x1 + 1);
        if (sq[i].x1 == sq[j].x1) tot -= 2;
        if (sq[i].x2 == sq[j].x2) tot -= 2;
      }
      if (sq[i].x2 + 1 == sq[j].x1) {  // vertical
        tot += 4 * (min(sq[i].y2, sq[j].y2) - max(sq[j].y1, sq[i].y1) + 1);
        if (sq[i].y1 == sq[j].y1) tot -= 2;
        if (sq[i].y2 == sq[j].y2) tot -= 2;
      }
    }
  }
  cout << tot / 2 << endl;
  return 0;
}

T2 我不会

pyt会讲

T3

考场思路：想到了与正解挺像的方法，并且在n%k==0时对了，因为脑子混乱而爆了个大零蛋

正解：cbx的神奇解法，因为题目中说按最大的数计算劳累程度，所以要想得到一个小数，那么这种情况一定全是小数。举个例子：如果m=3，想得到1，那么在每一位上都有 $ \frac{1}{m} $ 的几率是1，一共有K位，那么就有 $ (\frac{1}{m} )^2 $ 的几率结果得到1。如果想得到2，那么这个组合中只要有2就OK，所以概率为 $ \frac{2}{3} $ ，这种情况还包含了第一种为1的情况，所以最后还要减去它

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36


#include <bits/stdc++.h>
using namespace std;
const long long maxn = 1001, MOD = 1000000007;
long long qpow(long long base, long long power, long long mod) {
  if (power == 0) return 1;
  long long ans = 1;
  while (power) {
    if (power & 1) {
      ans = 1ll * ans * base % mod;
    }
    base = 1ll * (1ll * base * base) % mod;
    power >>= 1;
  }
  return ans;
}

long long n, m, k, fm, fz, fminv, ans;
long long w, franc[maxn], po[maxn];  //函数值 和 概率
int main() {
  cin >> n >> m >> k;
  fm = qpow(m, k, MOD);
  fminv = qpow(fm, MOD - 2, MOD);
  for (long long i = 1; i <= m; i++) {
    po[i] = (qpow(i, k, MOD) * fminv) % MOD;
    franc[i] = (po[i] - po[i - 1] + MOD) % MOD;
    cin >> w;
    ans = (ans + franc[i] * w % MOD) % MOD;
  }
  if (k > n) {
    cout << "0" << endl;
    return 0;
  }
  ans = ans * (n - k + 1) % MOD;
  cout << ans << endl;
  return 0;
}

T4

蓝书上有讲解，没啥好说的，代码我也码不对，Github上也有标程，不放了（PS：括号挺多，别打错了）

目录

noip模拟6

T1

T2 我不会

T3

T4