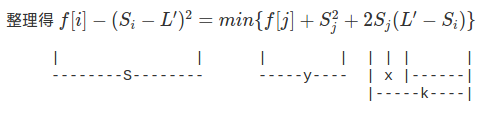0.关于斜率优化DP
特点:看起来很nb,如果打错了式子会很难调(我不看题解调不出来)

1.这道题的做法
emmm……先看最简单版的DP式子 $ f[i] = \min { f[j] + ( pre_i - pre_j + i - j - 1 - L)^2 } (j < i) $ 有点复杂,那就来简化一下,设 $ S_i = pre_i + i $ $ L' = L + 1 $
这样,原式= $ f[i] = min{ f[j] + (S_i-S_j-l')^2 } $
展开得 $ f[i] - (S_i - L')^2 = 2S_j(L'-S_i) + f[j] + S_j^2 $
整理得 
然后我们就得到了一个y = kx + b的函数图像 
我们的目的是让 b 最小,所以考虑找一个点过图像使它最小。
如图,我们将这个斜率为 $ k_i $ 的直线从下往上平移,直到有一个点 $ (x_p,y_p) $ 在这条直线上,则有 $b_i=y_p-k_ix_p$ ,这时 $ b_i $ 取到最小值。算完 $ f_i $ ,我们就把
这个点加入点集中,以做为新的 DP 决策。那么,我们该如何维护点集?
容易发现,可能让 $ b_i $ 取到最小值的点一定在下凸壳上。因此在寻找 $ p $ 的时候我们不需要枚举所有 $ i - 1 $ 个点,只需要考虑凸包上的点。而在本题中 $ k_i $ 随 $ i $的增加而递增,因此我们可以单调队列维护凸包。
具体地,设 $ K(a,b) $ 表示过 $(x_a, y_a)$ 和 $(x_b,y_b)$ 的直线的斜率。考虑队列 $q_l,q_{l+1},\ldots,q_r$ ,维护的是下凸壳上的点。也就是说,对于 $l<i<r$,始终有 $K(q_{i-1},q_i) < K(q_i,q_{i+1})$ 成立。
我们维护一个指针 $e$ 来计算 $b_i$ 最小值。我们需要找到一个 $K(q_{e-1},q_e)\le k_i< K(q_e,q_{e+1})$ 的 $e$(特别地,当 $e=l$ 或者 $e=r$ 时要特别判断),这时就有 $p=q_e$,即 $q_e$ 是 $i$ 的最优决策点。由于 $k_i$ 是单调递减的,因此 $e$ 的移动次数是均摊 $O(1)$ 的。
在插入一个点 $(x_i,y_i)$ 时,我们要判断是否 $K(q_{r-1},q_r)<K(q_r,i)$,如果不等式不成立就将 $q_r$ 弹出,直到等式满足。然后将 $i$ 插入到 $q$ 队尾。
OIwiki上的解释(我解释不清了(逃)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
#include <bits/stdc++.h>
using namespace std;
const long long maxn = 100010;
long long dp[maxn], pre[maxn], c[maxn], que[maxn];
long long n, l;
long long getS(long long id) { return pre[id] + id; }
long long getX(long long id) { return getS(id); }
long long getY(long long id) { return dp[id] + getS(id) * getS(id); }
long long getK(long long id) { return 2 * (getS(id) - l); }
long double getSL(long long i, long long j) {
return (long double)(getY(j) - getY(i)) / (getX(j) - getX(i));
}
int main() {
scanf("%lld%lld", &n, &l);
l++;
long long head, tail;
head = tail = 1;
for (long long i = 1; i <= n; i++) {
scanf("%lld", &c[i]);
pre[i] = pre[i - 1] + c[i];
}
for (long long i = 1; i <= n; i++) {
while (head < tail &&
getY(que[head + 1]) - getY(que[head]) -
(getX(que[head + 1]) - getX(que[head])) * getK(i) <
0)
head++;
dp[i] = getY(que[head]) - getK(i) * getX(que[head]) +
(getS(i) - l) * (getS(i) - l);
while (head < tail && (getY(que[tail]) - getY(que[tail - 1])) *
(getX(i) - getX(que[tail])) >=
(getY(i) - getY(que[tail])) *
(getX(que[tail]) - getX(que[tail - 1])))
tail--;
que[++tail] = i;
}
cout << dp[n] << endl;
return 0;
}
|