zkw线段树-洛谷日报
线段树的扩展之浅谈zkw线段树
posted on 2018-08-06 19:22:55 | under 线段树 | 29
0 阅读本文前请先阅读:
本文主要是上面文章的延伸,所以上文有讲的东西本文就不详细讲了QwQ
笔者的测试代码可能写丑了,所以如果慢请自行卡常QwQ
这里还是以**区间求和(RSQ)**为例
1 zkw线段树简介
什么是zkw线段树?
简单来说,就是非递归式线段树
众所周知,递归式线段树的常数很大,经常被卡,而zkw线段树的常数很小
这里用洛谷P3372做一个演示(更详细的补充见文末)
递归式线段树R9389075
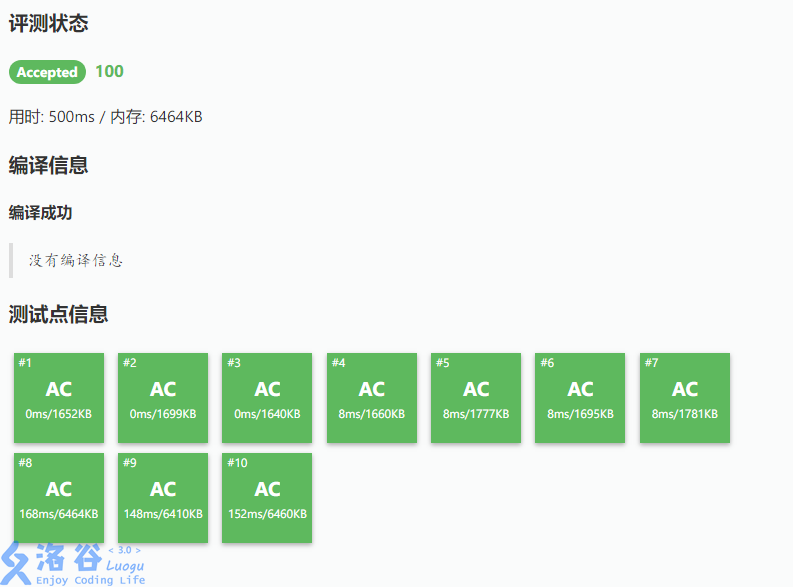
zkw线段树R9388963

前者运行时间是后者运行时间的2.05倍!Σ(°Д°;
测试用代码变量全部是unsigned long long类型的,如果按需调整速度还会更快
更详细的测试见3
其实zkw线段树不仅快,而且码量小(递归1.8KB,zkw1.48KB)、占用空间小(递归6.31MB,zkw4.94MB)、好调试吊打递归式线段树orz
而递归式线段树的优点则是方便理解与学习,并且适用范围更广一些(zkw线段树不能处理有运算优先级的问题,例如洛谷P3373(加法乘法混合处理) )
2 zkw线段树的实现
我们观察一下递归式线段树的代码,很容易就会发现:无论是建树、修改还是查询,都是自顶向下的。
zkw线段树则正好反过来,即自底向上
具体来说,就是先把线段树填充成满二叉树(堆式存储),之后就可以直接找到叶节点,然后回溯上去了
听起来好像很简单QwQ
其实真的很简单QwQ
2.1 先来看看怎么建树
首先是定义: /#define MAXN 200005 int tree[MAXN«2]; //tree是线段树数组 int n, N=1; //n是原数组实际长度,N下面会解释
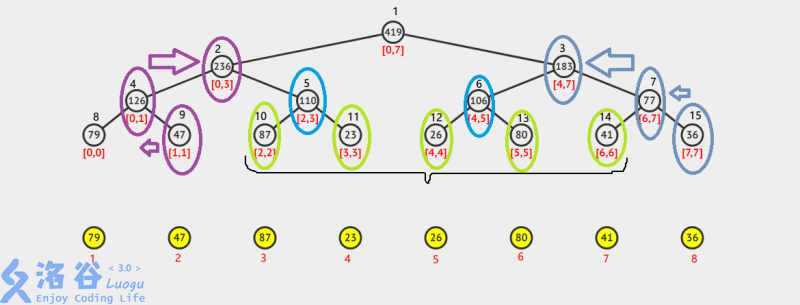
我们以下图为例
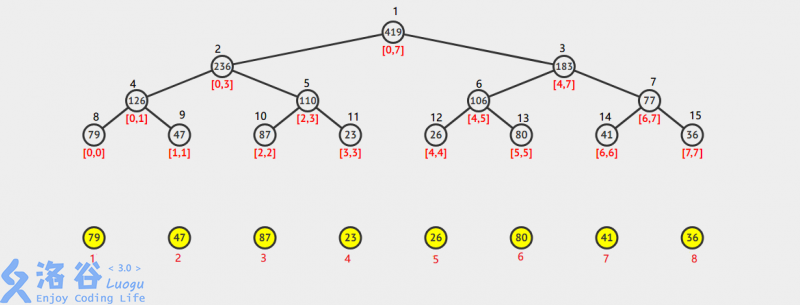
(由visualgo生成为了便于讲解,笔者做了一些改动QwQ)
如图,下面的黄圈是原数据,黄圈下面的红色数字是原数组的下标
上面的树就是线段树了,每一个节点内部都是节点下方标明的区间中所有元素的总和,上边的黑色数字就是线段树的下标
visualgo生成的数组下标默认是从0开始的,所以线段树下的区间和原数组有错位,请注意区分(笔者懒得改了
通过观察,我们发现一个规律:线段树对应叶子节点的下标和原数组的下标的差值是恒定的( 8−1=9−2=…=15−8=78-1=9-2=…=15-8=78−1=9−2=…=15−8=7)
这个差值就是一个和
N 很接近的数了(
N 是叶子节点数)
实际上,
N=2⌈log2(n+1)⌉N=2^{\lceil\log_2{(n+1)}\rceil}N=2⌈log2(n+1)⌉
根据这一点,我们可以这样建树:
/#define fp(i,l,r) for(register int i=(l);i<=(r);++i) /#define fd(i,r,l) for(register int i=(r);i>=(l);--i) /#define il inline //这个根据自己习惯调整,笔者习惯这么写了QwQ il void build(){ scanf("%d", &n); for(; N <= n+1; N <<= 1); //这个N当然可以直接算,不过为了算一个数就加一个/#include<cmath>有点不划算 fp(i, N+1, N+n) scanf("%d", tree+i); //这个等价于scanf("%d", &tree[i]) fd(i, N-1, 1) tree[i] = tree[i << 1] + tree[i << 1 | 1]; //这个等价于tree[i] = tree[i/*2] + tree[i/*2 + 1] }
大家可以和递归版线段树做一下对比
有细心的读者可能发现了:上例计算出的
N 是
16 而不是
8 !
还有,原数组在线段树对应的为止整体向后平移了1位!
其实这都是为了方便查找
后面再详细解释
2.2 接下来需要分成两个版本(单点修改+区间查询 和 区间修改+区间查询)
2.2.1 先说说单点修改+区间查询吧(Easy)
2.2.1.1 看看单点修改
实现很简单,所以直接放代码 il void modify(int x, int k){ for(x += N; x; x »= 1) tree[x] += k; }
完了?Σ(°Д°;
完了!
单点查询更简单,相信各位读者都能想到QwQ
2.2.1.2 再看看单点修改下的区间查询
我们以查询
[2,6] 为例(线段树上的,下同)
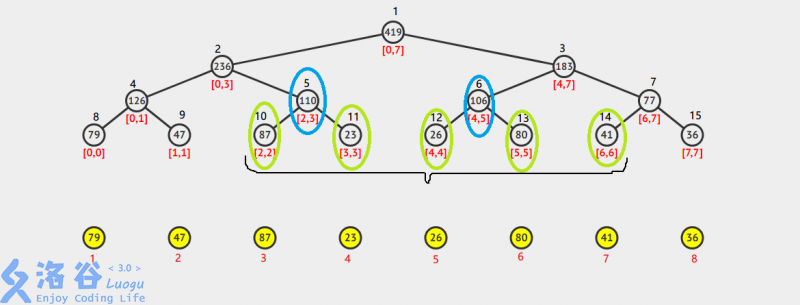
ans=[2,2]+[3,3]+[4,4]+[5,5]+[6,6]ans=\color{/#b5e61d}[2,2]+[3,3]+[4,4]+[5,5]+[6,6]ans=[2,2]+[3,3]+[4,4]+[5,5]+[6,6]
观察上图可以发现,因为在线段树上我们可以直接找到 [2,3]\color{/#00a2e8}[2,3][2,3]和 [4,5]\color{/#00a2e8}[4,5][4,5],所以我们只需要用 [2,3]\color{/#00a2e8}[2,3][2,3]代替 [2,2]\color{/#b5e61d}[2,2][2,2]和 [3,3]\color{/#b5e61d}[3,3][3,3];用 [4,5]\color{/#00a2e8}[4,5][4,5]代替 [4,4]\color{/#b5e61d}[4,4][4,4]和 [5,5]\color{/#b5e61d}[5,5][5,5]
于是
ans=[2,3]+[4,5]+[6,6]ans=\color{/#00a2e8}[2,3]+[4,5]\color{/#b5e61d}+[6,6]ans=[2,3]+[4,5]+[6,6]
自顶向下求和很简单,怎么实现自底向上的求和呢?
我们分别在区间左端点-1和右端点+1的位置放两个指针(令其为
s,t ),就像这样:
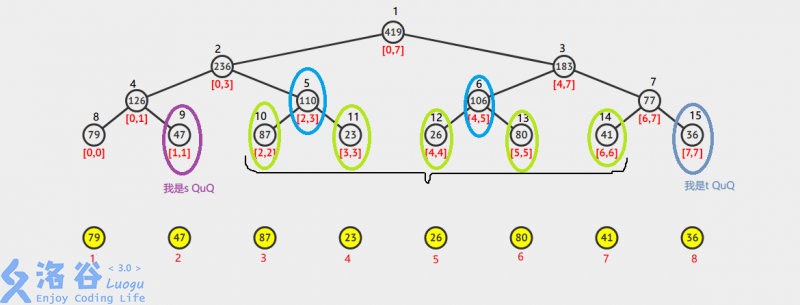
接着不断将
s,t 移动到对应节点的父节点处,直到
s,t 指向的节点的父节点相同时停止
在这期间,如果:
s 指向的节点是左儿子,那么
ans += 右儿子的值 1. t 指向的节点是右儿子,那么
ans += 左儿子的值
如果不能理解就看看上图,多看几遍就懂了QwQ
下面是代码 il int query(int s, int t){ int ans = 0; for(s = N + s - 1, r = N + r + 1; s ^ r ^ 1; s »= 1, r »= 1) { //这个for包含的信息量好像有点大,不过不要紧 //第一个分号前面就是将s和t初始化 //s ^ r ^ 1就是判断对应节点的父节点是否相同 //很容易看出来当对应节点互为左右儿子时,s^t = 1,再^1之后就是0 //而其他情况时,s^t大于1,^1后当然不是0 //第二个分号后面就是s,t上移 if(~s&1) ans += tree[s^1]; if(r&1) ans += tree[r^1]; //这两句的含义对照上面的实现过程看就能明白 } return ans; }
上面的那两个疑问现在可以解释了
仔细观察上述流程可以发现:我们只能查询
[1,n-1] 范围(这里还是线段树上标的)内的数据
如果我们想要查询
[0,m] 范围内( 0≤m≤n0\leq m\leq n0≤m≤n)的呢?
将数组整体平移!
如果我们想要查询
[m,n] 范围内( 0≤m≤n0\leq m\leq n0≤m≤n)的呢?
**把
N 直接扩大2倍!**
zkw:就是这么狠
到目前为止zkw线段树还是比较简短的
可能有人觉得这个和树状数组有点像,这就对了
zkw:树状数组究竟是什么?就是省掉一半空间后的线段树加上中序遍历
orz
单点修改+区间查询完结,整理一下代码:
//单点修改+区间查询 /#include
2.2.2 区间修改+区间查询(A little bit hard)
2.2.2.1 区间修改——噩梦的开始
很显然,我们不能用上面的方法暴力修改(还不如递归式线段树)
其实堆式存储也可以自顶向下访问
就是上下各走一次而已
但是我们有更好的办法 zkw:使劲想想就知道了
这里我们采用标记永久化的思想(就是不下推lazy tag让他彻底lazy下去QwQ) int add[MAXN«2]; //这个lazy tag表示当前节点已经更新完,需要更新子节点
我们需要在自底向上时更新节点的值,所以我们还需要一个变量记录该节点包含元素的个数
另外要注意修改某个节点的标记时要更新上面的值
举个例子;我们换一棵树
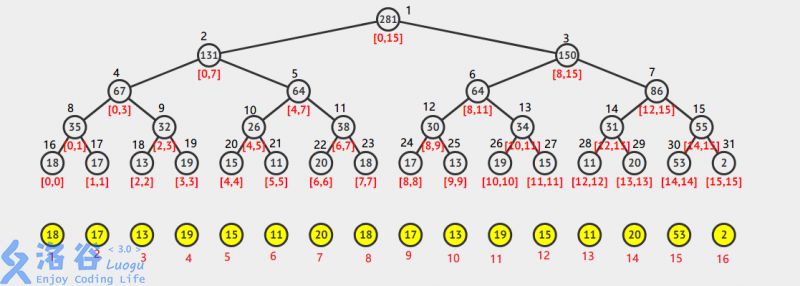
以修改
[2,10] 为例
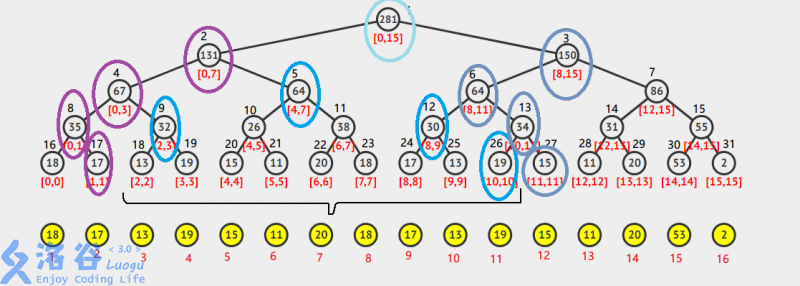
当
s 到了
[2,2] 节点时,
[3,3] 节点的add加
k ,那么接下来
[2,3] 、
[0,3] 节点的值都要加上
k/*1 ,而到了
[0,7] 节点时,因为
[4,7] 节点的add加了
k ,所以
[0,7] 节点的值要加上
k/*(1+4)=k/*5 ,自然
k 要乘的系数又需要一个变量来记录
需要注意的是,这次的修改要上推到根节点
下面是代码 il void update(int s, int t, int k){ int lNum=0, rNum=0, nNum=1; //lNum: s一路走来已经包含了几个数 //rNum: t一路走来已经包含了几个数 //nNum: 本层每个节点包含几个数 for(s = N+s-1, t = N+t+1; s^t^1; s »= 1, t »= 1, nNum «= 1) { //更新tree tree[s] += k/*lNum; tree[t] += k/*rNum; //处理add if(~s&1) {add[s^1] += k; tree[s^1] += k/*nNum; lNum += nNum;} if(t&1) {add[t^1] += k; tree[t^1] += k/*nNum; rNum += nNum;} } //更新上层tree for(; s; s »= 1, t »= 1) { tree[s] += k/*lNum; tree[t] += k/*rNum; } }
2.2.2.2 区间查询
我们以查询
[2,10] 为例没错笔者我就是用一张图

过程类似,要注意
s,t 每次上推时都要根据当前所在节点的标记和
lNum / rNum 更新
ans (
ans += add[s]/*lNum )
可能有些难懂,多读两遍或者看看代码或者自己手推一下就好了QwQ
同样,这个也需要上推到根节点 il int query(int s, int t){ int lNum=0, rNum=0, nNum=1; int ans=0; for(s = N+s-1, t = N+t+1; s^t^1; s »= 1, t »= 1, nNum «= 1) { //根据标记更新 if(add[s]) ans += add[s]/*lNum; if(add[t]) ans += add[t]/*rNum; //常规求和 if(~s&1) {ans += tree[s^1]; lNum += nNum;} if(t&1) {ans += tree[t^1]; rNum += nNum;} } //处理上层标记 for(; s; s »= 1, t »= 1) { ans += add[s]/*lNum; ans += add[t]/*rNum; } return ans; }
区间修改+区间查询到这里先告一段落,整理一下代码:
//区间修改+区间查询1 /#include
2.2.3 对区间修改+区间查询进行空间优化(A Little hard)
也许有的读者发现了:标记和值好像可以看成一个东西
所以,我们可不可以不存值,只存标记?
当然可以!
zkw:永久化的标记就是值!
zkw:狗拿耗子,猫下岗了
那么,怎么实现呢?
下面是区间最值(RMQ)版本的(以最小值为例)
在这里,我们不存总和了,存
tree[i]=sum[i]-sum[i»1] //sum[i]对应上述两个版本代码中的tree[i] (即为子节点-父节点)
区间修改就直接改
tree[i]
查询就从当前节点一直加到根(
tree[i]+tree[i»1]+…+tree[1] )
或者数学一点
∑j=0⌊log2i⌋tree[i»j]\displaystyle\sum_{\text{j}=0}^{\lfloor\log_2\text{i}\rfloor}\text{tree[i»j]}j=0∑⌊log2i⌋tree[i»j] (修改时的
s,t )遇到节点
x ,则
A=min(tree[x»1],tree[x»1|1]), tree[x]+=A, tree[x»1]-=A, tree[x»1|1]-=A
//这一步可能有一些难懂,就是修改了一个区间,可能会导致父节点存储的最值(普通情况下)发生改变,所以用这一步来修正
为什么笔者没有放区间求和(RSQ)版本的呢?
因为笔者发现区间求和版本的依然要维护两棵树(一棵存
tree[i]-tree[i-1] ,另一棵存
i/*(tree[i]-tree[i-1]) ,类似树状数组),也就是没有优化(可能是笔者太弱了,没有想到别的方法)
当然,这个版本也是可以单点修改/单点查询的,不过没有上述代码实用,所以这里就不讨论了
直接放代码 void build(){ for(N=1;N<=n+1;N«=1); fp(i,N+1,N+n) scanf("%d",tree+i); fd(i,N-1,1) { tree[i]=min(tree[i«1],tree[i«1|1]); tree[i«1]-=tree[i]; tree[i«1|1]-=tree[i]; } } void update(int s, int t, int k){ int tmp; for(s += N-1, t += N+1; s^t^1; s»=1, t»=1) { if(~s&1) tree[s^1]+=k; if(t&1) tree[t^1]+=k; tmp = min(tree[s], tree[s^1]); tree[s] -= tmp; tree[s^1] -= tmp; tree[s»1] += tmp; tmp = min(tree[t], tree[t^1]); tree[t] -= tmp; tree[t^1] -= tmp; tree[t»1] += tmp; } for (;s!=1;s»=1) { //记得要上推到根节点 tmp = min(tree[s],tree[s^1]); tree[s] -= tmp; tree[s^1] -= tmp; tree[s»1] += tmp; } } int query(int s, int t){ //闭区间 int sAns = 0, tAns = 0; s+=N, t+=N; if(s != t) { //防止查询单点时死循环 for(; s^t^1; s»=1, t»=1) { sAns += tree[s]; tAns += tree[t]; if(~s&1) sAns = min(sAns, tree[s^1]); if(t&1) tAns = min(tAns, tree[t^1]); } } int ans = min(sAns+tree[s], tAns+tree[t]); while(s > 1) ans += tree[s»=1]; return ans; }
3 大数据测试
当然,说好的大数据测试可不能忘
(2020.02.10 upd: 测试更新了)
先来看一看参赛选手:
1号:递归线段树
2号:zkw线段树(非差分版本,差分版本的常数略大,就不测了)
3号:树状数组
zkw线段树:说好的我的主场呢?
先以洛谷P3372做一个热身
因为图太多,所以不贴出来了,有兴趣的读者可以查看提交记录
读入优化
1号:递归线段树 412ms / 6.31MB (R9424058)
2号:zkw线段树 208ms / 4.74MB (R9424567)
3号:树状数组 196ms / 3.71MB (R9424624)
读入优化+O2
1号:递归线段树 220ms / 6.21MB (R9424921)
2号:zkw线段树 160ms / 4.86MB (R9424805)
3号:树状数组 96ms / 3.74MB (R9424762)
可以看到,没有O2时2号和3号相差无几,有了O2之后3号吊打全场可能是笔者写的zkw线段树常数太大QwQ
为了防止zkw线段树被吊打得太惨反应算法真实水平以及模拟NOIp竞赛环境,下面就不开O2了
在这里先放一下结果,测试代码和大数据放在另一篇文章里
保证所有输入数据在unsigned long long 范围内,结果对 2642^{64}264取模,表格中的时间为平均值
测试环境:
系统:noilinux-1.4.1(当然是虚拟机啦)
内存:2GB
CPU:AMD Athlon(tm) II X4 631 Quad-Core Processor 2600 MHz(就用了一个核)
请不要吐槽这个渣配置QwQ(话说这个配置和CCF老爷机的配置应该差不多吧)
顺便吐槽那个系统自带的辣鸡评测软件,一评测就闪退
测试/#1:
数据规模递归线段树(ms)zkw线段树(ms)树状数组(ms)5e5(5组)3554.3592067.9781968.0741e6(5组)7327.3444922.7254359.2725e6(3组)49416.19634078.83726782.1071e7(3组)126192.82074198.01557485.430
测试/#2(稍微卡卡常):
数据规模递归线段树(ms)zkw线段树(ms)树状数组(ms)5e5(5组)3985.4352085.2211981.1541e6(5组)6995.6114268.9883991.7245e6(3组)45401.98129582.95725179.3361e7(3组)99805.48867543.98554304.283
耗时: 树状数组≈zkw线段树<递归线段树\text{树状数组}\thickapprox\text{zkw线段树}<\text{递归线段树}树状数组≈zkw线段树<递归线段树
代码长度: 树状数组(1.57 KB)<zkw线段树(2.20 KB)<递归线段树(2.47 KB)\text{树状数组(1.57 KB)}<\text{zkw线段树(2.20 KB)}<\text{递归线段树(2.47 KB)}树状数组(1.57 KB)<zkw线段树(2.20 KB)<递归线段树(2.47 KB) (当然这个参考意义不大)
结论:不考虑有运算优先级的情况下,树状数组吊打全场(zkw线段树哭晕在厕所
4 后记
这篇文章笔者写了将近一天整整三天。通过写这篇文章,笔者对zkw线段树的理解更加深刻了顺便还学到了差分这个骚操作,并让树状数组吊打全场
当然,因为笔者是个蒟蒻,所以这篇文章难免会有错误,在此希望各位dalao批评的时候别把笔者喷得太惨QwQ
另外,zkw julao在他的ppt中还讲了许多高端操作,希望各位有兴趣读者能够看一看膜拜orz
关于线段树,还可以扩展出很多东西,比如多维线段树、多叉线段树、可持久化线段树……不过因为笔者是个蒟蒻,所以这些就先不写了
5 主要参考资料
- 统计的力量——线段树全接触(膜拜zkw julao)
- 线段树详解 (原理,实现与应用) - CSDN博客